Graph Algorithms
Why Graphs for Data Science?
Traditional data science and machine learning applications have relied on creating knowledge and understanding using columnar data. Each row of data (or each data point) is treated as independent from the others. However, there are many examples where considering the existing relationships between each data point can create more accurate models. Such examples include social network analysis, recommender systems, fraud detection, search, and question-answering bots.
This guide will walk you through some of the common algorithms that can be used in graph data science. In this guide, we will introduce you to how to use Neo4j Graph Data Science (GDS) to solve some common data science problems using graphs.
Neo4j Graph Data Science
Neo4j Graph Data Science (GDS) contains a set of graph algorithms, exposed through Cypher procedures. Graph algorithms provide insights into the graph structure and elements, for example, by computing centrality, similarity scores, and detecting communities.
This guide demonstrates the usual workflow for how to run production-tier algorithms. The generalized workflow is as follows:
-
Create a graph projection
-
Run a graph algorithm on a projection
-
Show and interpret example results
The official GDS documentation can be found here.
Graph Model
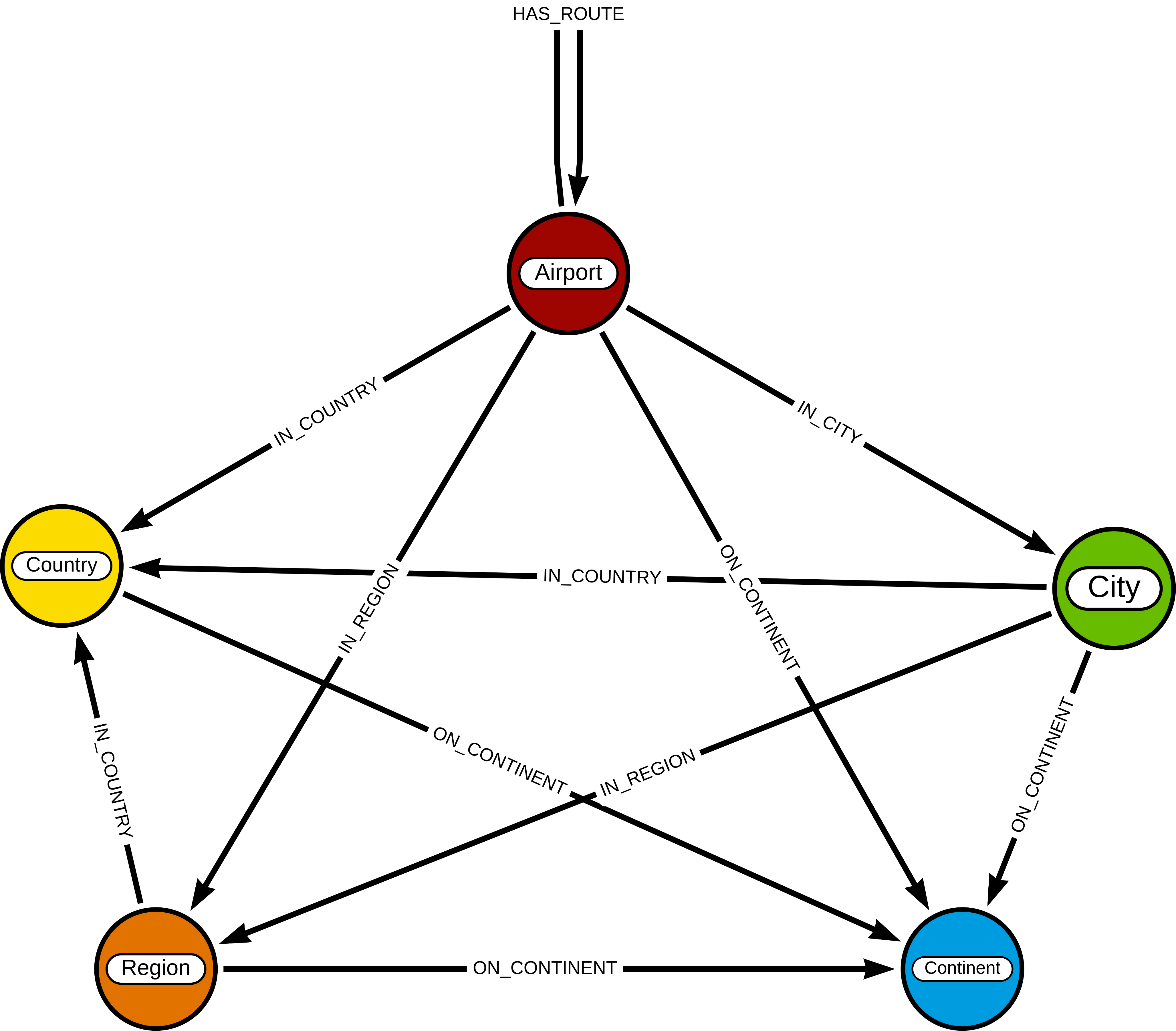
Before you run any of the algorithms, you need to import your data. We will be working with an example dataset that shows the connections between different airports across the world. Note that we have 5 different node labels (Airport, City, Country, Continent, and Region) and 5 different relationship types (:HAS_ROUTE, :IN_CITY, :IN_COUNTRY, :IN_REGION, and :ON_CONTINENT).
Attribution
This dataset was initially created by Kelvin Lawrence, available under the Apache License Version 2.0. The original dataset can be found GitHub repository and has been modified for the purposes of this guide.
Loading the data
We will use the Cypher command LOAD CSV to import our data into Neo4j from CSV file hosted on GitHub. It will parse a CSV file line by line as objects that can then be manipulated using Cypher.
We begin by creating uniqeness constraints on each of the nodes, which make for efficient queries.
CREATE CONSTRAINT airports IF NOT EXISTS ON (a:Airport) ASSERT a.iata IS UNIQUE;
CREATE CONSTRAINT cities IF NOT EXISTS ON (c:City) ASSERT c.name IS UNIQUE;
CREATE CONSTRAINT regions IF NOT EXISTS ON (r:Region) ASSERT r.name IS UNIQUE;
CREATE CONSTRAINT countries IF NOT EXISTS ON (c:Country) ASSERT c.code IS UNIQUE;
CREATE CONSTRAINT continents IF NOT EXISTS ON (c:Continent) ASSERT c.code IS UNIQUE;
Next we will import the Airport, Country, and Continent nodes and set their properties as well as the IN_CITY, IN_COUNTRY, IN_REGION and ON_CONTINENT relationships.
WITH
'https://raw.githubusercontent.com/neo4j-graph-examples/graph-data-science2/main/data/airport-node-list.csv'
AS url
LOAD CSV WITH HEADERS FROM url AS row
MERGE (a:Airport {iata: row.iata})
MERGE (ci:City {name: row.city})
MERGE (r:Region {name: row.region})
MERGE (co:Country {code: row.country})
MERGE (con:Continent {code: row.continent})
MERGE (a)-[:IN_CITY]->(ci)
MERGE (a)-[:IN_COUNTRY]->(co)
MERGE (ci)-[:IN_COUNTRY]->(co)
MERGE (r)-[:IN_COUNTRY]->(co)
MERGE (a)-[:IN_REGION]->(r)
MERGE (ci)-[:IN_REGION]->(r)
MERGE (a)-[:ON_CONTINENT]->(con)
MERGE (ci)-[:ON_CONTINENT]->(con)
MERGE (co)-[:ON_CONTINENT]->(con)
MERGE (r)-[:ON_CONTINENT]->(con)
SET a.id = row.id,
a.icao = row.icao,
a.city = row.city,
a.descr = row.descr,
a.runways = toInteger(row.runways),
a.longest = toInteger(row.longest),
a.altitude = toInteger(row.altitude),
a.lat = toFloat(row.lat),
a.lon = toFloat(row.lon);
Finally, we will import the (Airport)-[:HAS_ROUTE]-(Airport) relationship. Note that relationship has a property of distance, indicating the distance between each of the airports. We will later use this to create weighted graphs.
LOAD CSV WITH HEADERS FROM 'https://raw.githubusercontent.com/neo4j-graph-examples/graph-data-science2/main/data/iroutes-edges.csv' AS row
MATCH (source:Airport {iata: row.src})
MATCH (target:Airport {iata: row.dest})
MERGE (source)-[r:HAS_ROUTE]->(target)
ON CREATE SET r.distance = toInteger(row.dist);
Data visualization
Prior to running some algorithms, it is helpful to visualize our data. In order to do so, running the following query, which will give you the schema of the graph:
CALL db.schema.visualization()
Using this command, we can see our 5 different node and relationship types.
Summary statistics
Prior to using any of the GDS algorithms it can be beneficial to calculate some summary statistics on the data. For example, the following calculate the minimum, maximum, average, and standard deviation of the number of flights out of each airport.
MATCH (a:Airport)-[:HAS_ROUTE]->()
WITH a, count(*) AS num
RETURN min(num) AS min, max(num) AS max, avg(num) AS avg_routes, stdev(num) AS stdev
Graph creation
The first step in executing any GDS algorithm is to create a graph projection (also referred to as an in-memory graph) under a user-defined name. Graph projections, stored in the graph catalog under a user-defined name, are subsets of our full graph to be used in calculating results through the GDS algorithms. Their use enables GDS to run quickly and efficiently through the calculations. In the creation of these projections, the nature of the graph elements may change in the following ways:
-
Nodes and relationship types might be renamed
-
Several node or relationship types might be merged
-
The direction of relationships might be changed
-
Parallel relationships might be aggregated
-
Relationships might be derived from larger patterns
In this section we will explore how to project a graph using the native projection approach. It should be noted that graphs can also be create via Cypher projections, but these are beyond the scope of this guide.
Graph catalog: creating a graph with native projections
Native projections provide the fastest performance for creating an graph projection. They take 3 mandatory parameters: graphName, nodeProjection, and relationshipProjection. There are also optional configuration parameters that can be used to further configure the graph. In general, the syntax for creating a native projection is:
CALL gds.graph.project(
graphName: String,
nodeProjection: String or List or Map,
relationshipProjection: String or List or Map,
configuration: Map
)
YIELD
graphName: String,
nodeProjection: Map,
nodeCount: Integer,
relationshipProjection: Map,
relationshipCount: Integer,
projectMillis: Integer,
createMillis: Integer
Example of a native projection
In our dataset, we could create a graph projection of the routes between all airports as:
CALL gds.graph.project(
'routes',
'Airport',
'HAS_ROUTE'
)
YIELD
graphName, nodeProjection, nodeCount, relationshipProjection, relationshipCount
This is a very simple graph projection, but it is possible to add multiple node types and relationship types as well as properties for each of the nodes and relationships. To see more examples of creating native graph projections, consult the GDS documentation.
Graph catalog: listing and existence
It is helpful to know which graphs are in the catalog and their properties. To see this for all graphs, you use
CALL gds.graph.list()
You can also check this for an individual graph using:
CALL gds.graph.list('graph-name')
where graph-name is the name of your projected, in-memory graph.
Algorithm syntax: available execution modes
Once you have created a named graph projection, there are 4 different execution modes provided for each algorithm:
-
stream: Returns the results of the algorithm as a stream of records without altering the database -
write: Writes the results of the algorithm to the Neo4j database and returns a single record of summary statistics -
mutate: Writes the results of the algorithm to the projected graph and returns a single record of summary statistics -
stats: Returns a single record of summary statistics but does not write to either the Neo4j database or the projected graph
In addition to the above for modes, it is possible to use estimate to obtain an estimation of how much memory a given algorithm will use.
A special note on mutate mode
When it comes time for feature engineering, you will likely want to include some quantities calculated by GDS into your graph projection. This is what mutate is for. It does not change the database itself, but writes the results of the calculation to each node within the projected graph for future calculations. It is beyond the scope of this guide, but is covered in more detail in the API docs.
Algorithm syntax: general algorithm use
Utilizing one of the 4 different execution modes, the general way to call a graph algorithm is as follows:
CALL gds[.<tier>].<algorithm>.<execution-mode>[.<estimate>]( graphName: String, configuration: Map )
where items in [] are optional. <tier>, if present, indicates whether the algorithm is in the alpha or beta tier (production-tiered algorithms do not use this), <algorithm> is the name of the algorithm, <execution-mode> is one of the 4 execution modes, and <estimate> is an optional flag indicating that the estimate of memory usage should be returned.
Centrality measurements via PageRank

There are many ways to determine the centrality or importance of a node, but one of the most popular is through the calculation of PageRank. PageRank measures the transitive (or directional) influence of a node. The benefit to this approach is that it uses the influence of a node’s neighbors to determine the influence of the target node. The general idea is that a node that has more incoming and more influential links from other nodes is considered to be more important (i.e. a higher PageRank).
The algorithm itself is an iterative algorithm. The number of iterations can be set as a configuration parameter in GDS, however the algorithm can terminate if the node scores converge based on a specified tolerance value, which is also configurable in GDS.
PageRank example graph
We will utilize the routes graph projection that we wrote before. If you need to recreate that graph projection, you can do so with the following:
CALL gds.graph.project(
'routes',
'Airport',
'HAS_ROUTE'
)
YIELD
graphName, nodeProjection, nodeCount, relationshipProjection, relationshipCount
PageRank: stream mode
As previously stated, stream mode will output the results of the calculation without altering the database or the graph projection. To do so, we use:
CALL gds.pageRank.stream('routes')
YIELD nodeId, score
RETURN gds.util.asNode(nodeId).iata AS iata, gds.util.asNode(nodeId).descr AS description, score
ORDER BY score DESC, iata ASC
Here we see that we have returned the results of the calculation, mapped in the internal id space, as well as the PageRank score. We then extract the iata code of the airport from the id space using gds.util.asNode(). We can see that the output is the airport codes, ordered by decreasing PageRank score. The airports with the highest PageRank scores are very popular airports around the globe, as we would expect.
Note that PageRank can also be run on a basic graph, such as what we are using here, or with a weighted graph. To see how to run it on a weighted graph, please explore the GDS documentation.
Interpretting results of an algorithm
GDS uses an internal id space for its calculations, which does not correspond to recognizable information of the graph itself. As such, when we return results from an algorithm, it is returned in the id space. We generally want to convert this to something coresponding to our actual graph. To do so, we use the built in method:
gds.util.asNode(nodeId).property_name AS property_name
which will extract the desired property_name from the graph projection based on the id space. We will see examples of this shortly.
PageRank: write mode
If we want to attach the results of the PageRank calculation as a node property to each node in the graph, we would use .write() as follows:
CALL gds.pageRank.write('routes',
{
writeProperty: 'pagerank'
}
)
YIELD nodePropertiesWritten, ranIterations
We can then confirm the results using:
MATCH (a:Airport)
RETURN a.iata AS iata, a.descr AS description, a.pagerank AS pagerank
ORDER BY a.pagerank DESC, a.iata ASC
As we can see, the results are identical to the streamed version.
Community (cluster) detection via Louvain Modularity
As with centrality measurements, there are many ways to identify communities within a graph. Community detection is a useful tool for identifying regions of a graph that are densely clustered. For example, in our airport routes graph, it would help us find regions of the globe where airports have high travel rates between or where airports form natural clusters based on the density of airports in a region.
We will cover the popular Louvain Modularity method in this section. This algorithm finds clusters within a graph by measuring the density of nodes. This is quantified through the modularity, which is a comparison of the density of connections within a cluster to an average or random sample. So the higher the modularity, the more dense the cluster is. The Louvain method thus attempts to maximize the modularity across the graph through a recursive approach. As with PageRank, in GDS the user can specify a maximum number of iterations as well as a tolerance factor for early termination. Additionally, the algorithm is able to return the intermediate community assignments along the way to convergence.
Louvain example graph
We will utilize the routes graph projection that we wrote before. If you need to recreate that graph projection, you can do so with the following:
CALL gds.graph.project(
'routes',
'Airport',
'HAS_ROUTE'
)
YIELD
graphName, nodeProjection, nodeCount, relationshipProjection, relationshipCount
Louvain: example
Using the stream mode, let’s explore the results of the algorithm. We will use the following query:
CALL gds.louvain.stream('routes')
YIELD nodeId, communityId
RETURN
communityId,
SIZE(COLLECT(gds.util.asNode(nodeId).iata)) AS number_of_airports,
COLLECT(gds.util.asNode(nodeId).city) AS city
ORDER BY number_of_airports DESC, communityId;
In this case we have obtained the community IDs and counted the number of airports, by iata code, in each community using the combination of COLLECT, which creates a list of the results, and SIZE, which returns the size of a list. We also return a list of the cities in each community.
Exploring this list, we can see that the largest community corresponds to airports in the United States, the second largest to airports in Europe, and so on. At surface inspection, these results make sense in that the airports in the graph appear to be clustered based on continent.
As before, should we wish to write these results as node properties, we can use gds.louvain.write().
Node similarity
As with the previous algorithm categories of centrality and community detection, there are various ways to calculate node similarity. In general, node similarity is computed between pairs of nodes through different vector-based metrics. This is useful for things like recommendation engines where you want to, for example, recommend similar objects to purchase based on a customer’s previous purchases. In this section we will use a common approach to calculating pair-wise similarity that uses the Jaccard similarity score.
Node similarity considers every relationships between every node. If there is a relationship between nodes n and m, the algorithm then explores the other relationships individually of these two nodes. The percentage overlap in these individual sets is returned as the node similarity, where high similarities are near 1.0.
It should be noted that running node similarity scales quadratically with the number of nodes in the graph. To help minimize the run time, particularly on larger graphs, it is possible to set cutoffs on the degree of the nodes (the number of incoming or outgoing relationships) as well as a similarity cutoff. This then reduces the number of pair-wise combinations that must be evaluated. The result limits can either be set on the whole graph (referred to as N in the documentation) or to the results per node (referred to as K in the documentation).
Node similarity: example graph
We will utilize the routes graph projection that we wrote before. If you need to recreate that graph projection, you can do so with the following:
CALL gds.graph.project(
'routes',
'Airport',
'HAS_ROUTE'
)
YIELD
graphName, nodeProjection, nodeCount, relationshipProjection, relationshipCount
Node similarity: simple example
Let’s look at an example of a very basic node similarity calculation:
CALL gds.nodeSimilarity.stream('routes')
YIELD node1, node2, similarity
RETURN
gds.util.asNode(node1).city AS City1,
COLLECT(gds.util.asNode(node2).city) AS City2,
COLLECT(similarity) AS similarity
ORDER BY City1
We see that the algorithm has returned the top 10 most similar nodes for each airport node in the graph. What has happened here behind the scenes is that GDS has limited, on a per node basis (K), the number of results being returned, established by the configuration parameter topK, which has a default value of 10. We could restrict this further by altering the above query as:
CALL gds.nodeSimilarity.stream(
'routes',
{
topK: 3
}
)
YIELD node1, node2, similarity
RETURN
gds.util.asNode(node1).city AS City1,
COLLECT(gds.util.asNode(node2).city) AS City2,
COLLECT(similarity) AS similarity
ORDER BY City1
Node similarity: topN and bottomN
As previously stated, we can limit the number of similarity scores across all nodes by specifying topN, the largest overall similarity scores in the graph. As example of this would be:author:
CALL gds.nodeSimilarity.stream(
'routes',
{
topK: 1,
topN: 10
}
)
YIELD node1, node2, similarity
RETURN
gds.util.asNode(node1).city AS City1,
COLLECT(gds.util.asNode(node2).city) AS City2,
COLLECT(similarity) AS similarity
ORDER BY City1
In this case, we have calculated the airport with the highest similarity for each node (topK: 1) and then returned the 10 airport pairs with the highest similarity across the whole graph (topN: 10).
Node similarity: degree and similarity cutoff
Another way of limiting the number of calculations done is to provide a minimum value of degree for a node to be considered in the overall calculations, such as below where we require a minimum degree of 100 (i.e. a minimum of 100 flights coming in to and out of an airport):
CALL gds.nodeSimilarity.stream(
'routes',
{
degreeCutoff: 100
}
)
YIELD node1, node2, similarity
RETURN
gds.util.asNode(node1).city AS City1,
COLLECT(gds.util.asNode(node2).city) AS City2,
COLLECT(similarity) AS similarity
ORDER BY City1
We can also set a minimum similarity score:
CALL gds.nodeSimilarity.stream(
'routes',
{
similarityCutoff: 0.5
}
)
YIELD node1, node2, similarity
RETURN
gds.util.asNode(node1).city AS City1,
COLLECT(gds.util.asNode(node2).city) AS City2,
COLLECT(similarity) AS similarity
ORDER BY City1
Path Finding
Like all of the other algorithm categories we have explored, there are several approaches possible for path finding. Generally speaking, the purpose of path finding is to find the shortest path between two or more nodes. In the case of our airport route graph, this would help us identify which airport connections would be required to minimize the overall flight distance.
In this section we will use the common Dijkstra’s algorithm to find the shortest path between two nodes. Unlike the previous examples, we will need a weighted graph projection because Dijkstra’s algorithm begins by finding the lowest weighted relationship from the source nodes to all nodes that are directly connected to it. It then performs the same calculation from that node to all nodes connected to it, and so on, always choosing the relationship with the lowest weight, until the target node is reached.
Creating a weighted graph projection
In our previous examples we did not consider the distance between the two airports, which we will use for calculating shortest paths based on distance. We need to begin by creating a graph projection using the distance as the weight of the relationship between two nodes. In order to create a graph identical to our previous one with the simple addition of relationship weights, we would use:
CALL gds.graph.project(
'routes-weighted',
'Airport',
'HAS_ROUTE',
{
relationshipProperties: 'distance'
}
)
Dijkstra’s algorithm: calculating the shortest path given a source node
Let’s calculate the shortest distance from the Denver International Airport (DEN) to the Malé International Airport (MLE) using our weighted graph projection:
MATCH (source:Airport {iata: 'DEN'}), (target:Airport {iata: 'MLE'})
CALL gds.shortestPath.dijkstra.stream('routes-weighted', {
sourceNode: source,
targetNode: target,
relationshipWeightProperty: 'distance'
})
YIELD index, sourceNode, targetNode, totalCost, nodeIds, costs, path
RETURN
index,
gds.util.asNode(sourceNode).iata AS sourceNodeName,
gds.util.asNode(targetNode).iata AS targetNodeName,
totalCost,
[nodeId IN nodeIds | gds.util.asNode(nodeId).iata] AS nodeNames,
costs,
nodes(path) as path
ORDER BY index
We can see in the above query that we are specifying a source and target node and using the relationshipWeightProperty of distance. From there, many things are returned, including the total cost (similar to distance, usually representing the straight-line distance between two nodes while ignoring other potential sources of delay such as time spent taxiing, etc.), and a listing of the airports along this path. In this case, we see that the shortest path is 4 hops long — perhaps not practical, but the total distance is minimized.
Identifying appropriate algorithms for your graph

Not all GDS algorithms will run on every type of graph projection. Some algorithms prefer homogeneous to heterogeneous graphs. Others will only work properly on undirected graphs. Some will not work with relationships weights. You should always consult the API docs for your chosen algorithm to verify what is required for your graph.
Cleaning up
To free up memory, do not forget to drop your unused graph projections!
CALL gds.graph.drop('routes');
CALL gds.graph.drop('routes-weighted');
The end
Congratulations! You have taken your first steps into using Neo4j Graph Data Science! This tutorial just looked at the basics of how to run graph algorithms and demonstrated the approach on a very limited number of basic algorithms. To learn more about what other algorithms exists as well as details for all of their configurations, please see the GDS documentation.
Next steps
If you would like to work efficiently with larger graphs using a fully-managed cloud service, then check out AuraDS! Alternatively, you can also explore more in the Neo4j Sandbox, Neo4j Desktop, or Docker^.